Note

Click here to download the full example code

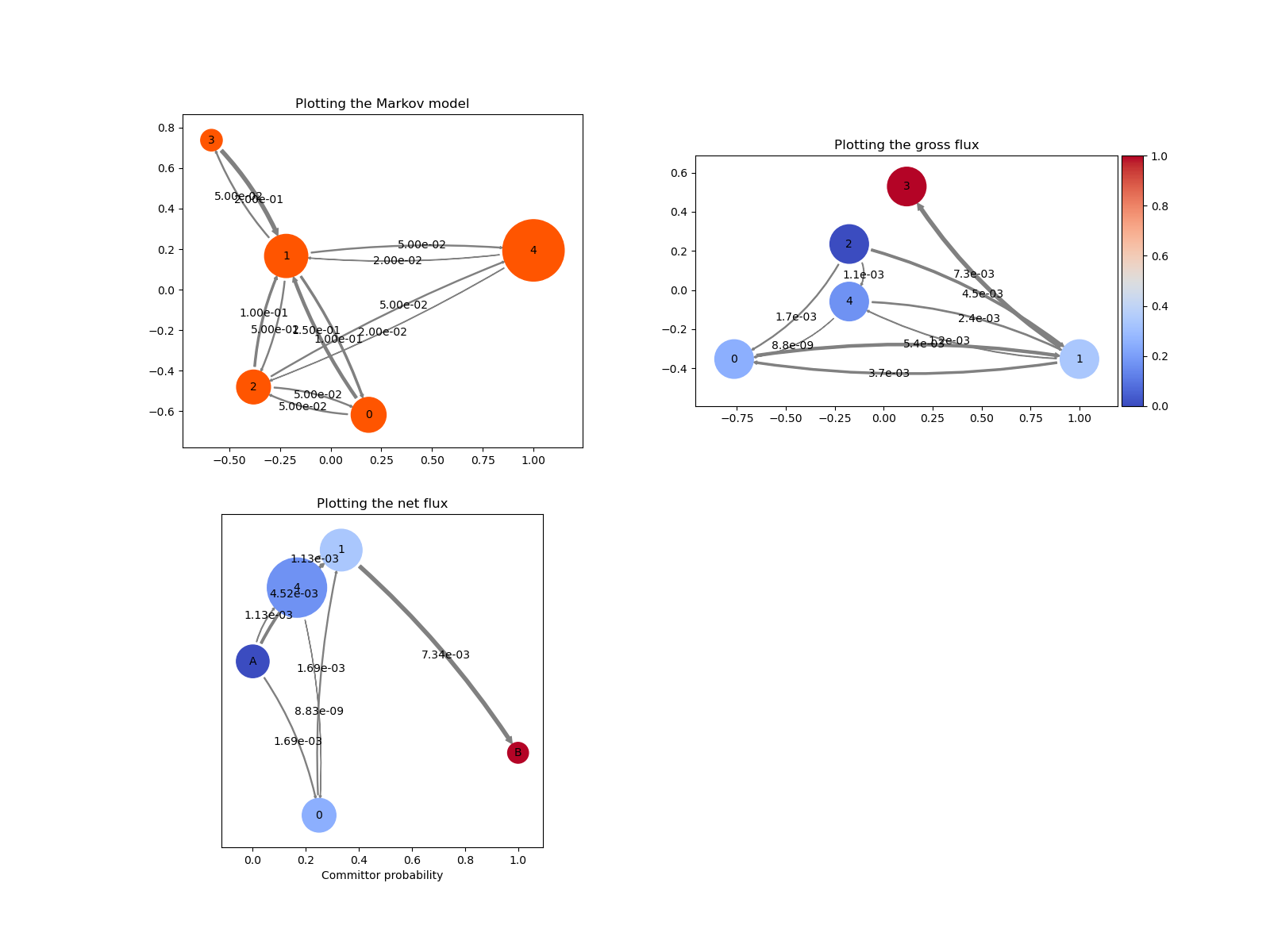
Network plots

We demonstrate different kinds of network plots based on plots.Network. In particular:

  • plotting a Markov state model where the state sizes depend on the stationary distribution and edges are scaled according to jump probabilities (deeptime.plots.plot_markov_model())

  • plotting the gross flux, in accordance to edge widths and colored according to the forward committor (deeptime.plots.Network()).

Plotting the Markov model, Plotting the gross flux, Plotting the net flux
13 import numpy as np
14 import matplotlib as mpl
15 import matplotlib.pyplot as plt
16 import networkx as nx
17
18 from mpl_toolkits.axes_grid1 import make_axes_locatable
19
20 from deeptime.markov.msm import MarkovStateModel
21 from deeptime.plots import plot_markov_model, Network, plot_flux
22
23 P = np.array([[0.8, 0.15, 0.05, 0.0, 0.0],
24               [0.1, 0.75, 0.05, 0.05, 0.05],
25               [0.05, 0.1, 0.8, 0.0, 0.05],
26               [0.0, 0.2, 0.0, 0.8, 0.0],
27               [1e-7, 0.02 - 1e-7, 0.02, 0.0, 0.96]])
28
29 f, axes = plt.subplots(2, 2, figsize=(16, 12))
30 for ax in axes.flatten():
31     ax.set_aspect('equal')
32
33 ax = axes[0][0]
34 ax.set_title('Plotting the Markov model')
35 plot_markov_model(P, ax=ax)
36
37 ax = axes[0][1]
38 ax.set_title('Plotting the gross flux')
39 flux = MarkovStateModel(P).reactive_flux(source_states=[2], target_states=[3])
40 positions = nx.planar_layout(nx.from_numpy_array(flux.gross_flux))
41 cmap = mpl.cm.get_cmap('coolwarm')
42 network = Network(flux.gross_flux, positions, edge_curvature=2.,
43                   state_colors=flux.forward_committor, cmap=cmap)
44 network.plot(ax=ax)
45 norm = mpl.colors.Normalize(vmin=np.min(flux.forward_committor), vmax=np.max(flux.forward_committor))
46 divider = make_axes_locatable(ax)
47 cax = divider.append_axes("right", size="5%", pad=0.05)
48 f.colorbar(mpl.cm.ScalarMappable(norm, cmap), cax=cax)
49
50 ax = axes[1][0]
51 ax.set_title('Plotting the net flux')
52 ax.get_yaxis().set_visible(False)
53 plot_flux(flux, attribute_to_plot='net_flux', ax=ax)
54
55 f.delaxes(axes[1][1])

Total running time of the script: ( 0 minutes 1.342 seconds)

Estimated memory usage: 9 MB