SINDy: Identification of the Rössler system

This example shows how to use SINDy to discover the chaotic Rossler system from measurement data via the deeptime.sindy.SINDy estimator and deeptime.sindy.SINDyModel model. Once we’ve learned the system, we can also simulate forward in time from novel initial conditions.

Note that for this example we pass in the exact derivatives. In practice one can also pass in a numerical approximation in their place.

• 
• 

x' = -1.000 x1 + -1.000 x2
y' = 1.000 x0 + 0.100 x1
z' = 0.100 1 + -14.000 x2 + 1.000 x0 x2

import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
from sklearn.preprocessing import PolynomialFeatures

from deeptime.sindy import SINDy, STLSQ


# Generate measurements of the Rossler system
a = 0.1
b = 0.1
c = 14


def rossler(z, t):
    return [-z[1] - z[2], z[0] + a * z[1], b + z[2] * (z[0] - c)]


dt = 0.01
t_train = np.arange(0, 150, dt)
x0_train = [-1, -1, 0]
x_train = odeint(rossler, x0_train, t_train)
x_dot_train = np.array([rossler(xi, 1) for xi in x_train])

# Plot training data
fig = plt.figure(figsize=(8, 6))
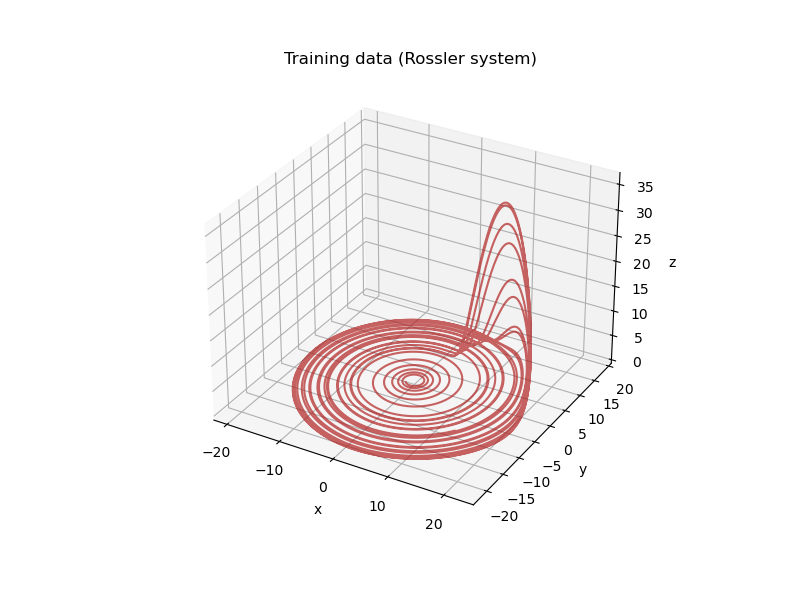
ax = fig.add_subplot(111, projection="3d")
ax.plot(x_train[:, 0], x_train[:, 1], x_train[:, 2], color="firebrick", alpha=0.7)
ax.set(xlabel="x", ylabel="y", zlabel="z", title="Training data (Rossler system)")

# Instantiate and fit an estimator to the data
estimator = SINDy(
    library=PolynomialFeatures(degree=3),
    optimizer=STLSQ(threshold=0.05),
)
estimator.fit(x_train, y=x_dot_train)

# Get the underlying ODE model
model = estimator.fetch_model()
model.print(lhs=["x", "y", "z"])

# Simulate from novel initial conditions
t_test = t_train
x0_test = [2, 3, 0]
x_test = odeint(rossler, x0_test, t_test)

# Plot test data
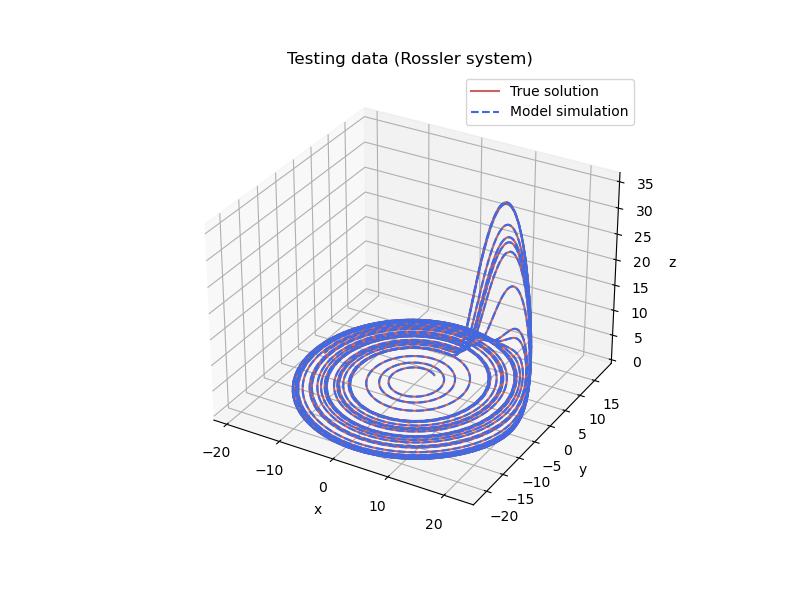
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection="3d")
ax.plot(x_test[:, 0], x_test[:, 1], x_test[:, 2], label="True solution", color="firebrick", alpha=0.7)
ax.set(xlabel="x", ylabel="y", zlabel="z", title="Testing data (Rossler system)")

# Simulate data with SINDy model and plot
x_sim = model.simulate(x0_test, t_test)
ax.plot(x_sim[:, 0], x_sim[:, 1], x_sim[:, 2], label="Model simulation", color="royalblue", linestyle="dashed")
ax.legend()

Estimated memory usage: 9 MB