Note
Click here to download the full example code
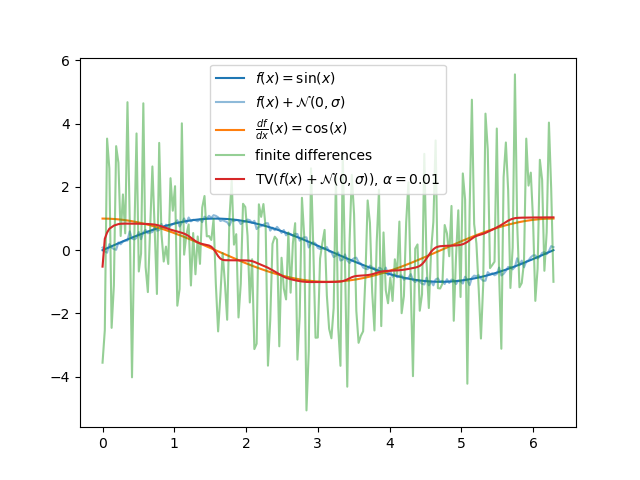
TV Derivative¶
Total-variation regularized derivative on a noisy function.
8 import numpy as np
9 import deeptime.util.diff as diff
10 import matplotlib.pyplot as plt
11
12 noise_variance = .08 * .08
13 x0 = np.linspace(0, 2.0 * np.pi, 200)
14 testf = np.sin(x0) + np.random.normal(0.0, np.sqrt(noise_variance), x0.shape)
15 true_deriv = np.cos(x0)
16 df_tv = diff.tv_derivative(x0, testf, alpha=0.001, tol=1e-5, fd_window_radius=5, sparse=False)
17
18 plt.figure()
19 plt.plot(x0, np.sin(x0), label=r'$f(x) = \sin(x)$')
20 plt.plot(x0, testf, label=r'$f(x) + \mathcal{N}(0, \sigma)$', color='C0', alpha=.5)
21 plt.plot(x0, true_deriv, label=r'$\frac{df}{dx}(x) = \cos(x)$')
22 plt.plot(x0, np.gradient(testf, x0), label='finite differences', alpha=.5)
23 plt.plot(x0, df_tv, label=r'$\mathrm{TV}(f(x) + \mathcal{N}(0, \sigma))$, $\alpha = 0.01$')
24 plt.legend()
Total running time of the script: ( 0 minutes 0.770 seconds)
Estimated memory usage: 8 MB
