function prinz_potential

deeptime.data.prinz_potential(h=1e-05, n_steps=500, temperature_factor=1.0, mass=1.0, damping=1.0)

Particle diffusing in a one-dimensional quadruple well potential landscape. [1]

The potential is defined as

\[V(x) = 4 \left( x^8 + 0.8 e^{-80 x^2} + 0.2 e^{-80 (x-0.5)^2} + 0.5 e^{-40 (x+0.5)^2}\right). \]

The integrator is an Euler-Maruyama type integrator, updating the current state \(x_t\) via

\[x_{t+1} = x_t - \frac{h\nabla V(x_t)}{m\cdot d} + \sqrt{2\frac{h\cdot\mathrm{kT}}{m\cdot d}}\eta_t, \]

where \(m\) is the mass, \(d\) the damping factor, and \(\eta_t \sim \mathcal{N}(0, 1)\).

The locations of the minima can be accessed via the minima attribute.

(Source code, png, hires.png, pdf)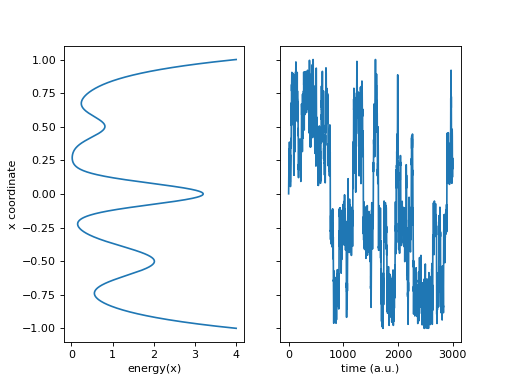

../../_images/plot_prinz.png
Parameters:

  • h (float, default=1e-5) – The integrator step size. If the temperature is too high and the step size too large, the integrator may produce NaNs.

  • n_steps (int, default=500) – Number of integration steps between each evaluation of the system’s state.

  • temperature_factor (float, default=1) – The temperature kT.

  • mass (float, default=1) – The particle’s mass.

  • damping (float, default=1) – Damping factor.

Returns:

system – The system.

Return type:

TimeIndependentSystem

Examples

The model possesses the capability to simulate trajectories as well as be evaluated at test points:

>>> import numpy as np
>>> from deeptime.data import prinz_potential

First, set up the model (which internally already creates the integrator).

>>> model = prinz_potential(h=1e-3, n_steps=100)  # create model instance

Now, a trajectory can be generated:

>>> traj = model.trajectory(np.array([[-0.]]), 1000, seed=42, n_jobs=1)  # simulate trajectory
>>> assert traj.shape == (1000, 1)  # 1000 evaluations from initial condition [0]

Or, alternatively the model can be evaluated at test points (mapping forward using the dynamical system):

>>> test_points = np.random.uniform(.5, 1.5, (100, 1))  # 100 test points
>>> evaluations = model(test_points, seed=53, n_jobs=1)
>>> assert evaluations.shape == (100, 1)

We can obtain the x-coordinates of the energy minima via the minima attribute:

>>> model.minima
array([-0.73943019, -0.22373758,  0.26914935,  0.67329635])

References