MSM on Prinz potential

In this example we study the estimation of a Markov state model based on particles living in the Prinz potential landscape.

from matplotlib import pyplot as plt
import numpy as np

from deeptime.clustering import BoxDiscretization
from deeptime.markov import TransitionCountEstimator
from deeptime.markov.msm import MaximumLikelihoodMSM
from deeptime.data import prinz_potential

First, we create the Prinz potential system and generate a plot of its potential function.

prinz_system = prinz_potential()

xs = np.linspace(-1., 1., 500)
ys = prinz_system.potential(xs)
plt.plot(xs, ys)
plt.xlabel('x')
plt.ylabel('V(x)');

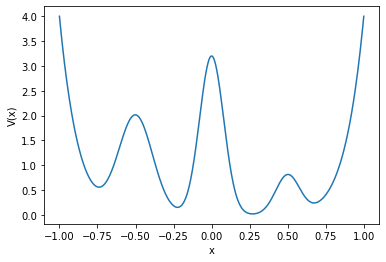
Now we can simulate trajectories for 50 particles, each starting in the origin \(x=0\) and generating 20000 frames.

data = prinz_system.trajectory(np.zeros((50, 1)), 20000)
print(f"Output shape {data.shape} for {data.shape[0]} particles, {data.shape[1]} frames "
      f"in {data.shape[2]} dimension.")

Output shape (50, 20000, 1) for 50 particles, 20000 frames in 1 dimension.

A histogram over the obtained data reflects the (inverse) potential landscape.

plt.hist(np.concatenate(data), bins=150);

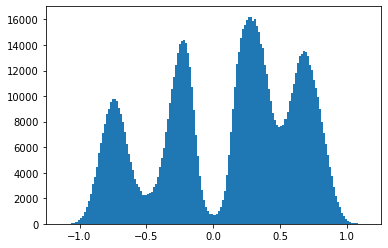
We want to generate a sequence of MSMs under lagtime \(\tau=2\) and varying accuracy regarding the spatial clustering.

lag = 2
n_clusters = [5, 7, 10, 15, 30, 50]

Each number of clusters yields a discretization which we use to build a MSM.

clusterings, msms = [], []

for n in n_clusters:
    cluster = BoxDiscretization(1, n, v0=[-1], v1=[1]).fit_fetch(np.concatenate(data))
    clusterings.append(cluster)

    dtrajs = [cluster.transform(x) for x in data]

    count_model = TransitionCountEstimator(lag, 'sliding').fit_fetch(dtrajs)
    msm = MaximumLikelihoodMSM().fit_fetch(count_model.submodel_largest())
    msms.append(msm)

We can now look at different properties of the estimated MSMs.

The transition matrices from coarse to fine with states ordered from left to right in configuration space:

f, axes = plt.subplots(nrows=2, ncols=int(len(msms)//2), figsize=(8, 5))

for ax, msm in zip(axes.flatten(), msms):
    ax.imshow(msm.transition_matrix, cmap=plt.cm.Greys)
    ax.set_xticks([])
    ax.set_yticks([])
    ax.set_title(f'n = {msm.n_states}')

The stationary distribution and first three nontrivial eigenfunctions:

n_eigenfunctions = 4
cmap = plt.cm.Set1

f, axes = plt.subplots(nrows=n_eigenfunctions, ncols=len(msms), figsize=(16, 8), sharex=True, sharey=True)

finest_cl = clusterings[-1]
finest_msm = msms[-1]

for n, (msm, cluster) in enumerate(zip(msms, clusterings)):
    eigenvectors = msm.eigenvectors_left()
    for eig_n in range(n_eigenfunctions):
        ax = axes[eig_n, n]

        y = eigenvectors.T[:, eig_n]
        y = 2*(y-y.min())/(y.max() - y.min()) - 1  # rescale

        y0_ = finest_msm.eigenvectors_left().T[:, eig_n] / finest_msm.eigenvectors_left().T[:, eig_n].max()
        y0 = np.interp(cluster.cluster_centers[:, 0], finest_cl.cluster_centers[:, 0], y0_)

        if ((-y-y0)**2).sum() < ((y-y0)**2).sum():
            y = -y

        ax.step(cluster.cluster_centers[:, 0], y, color=cmap(eig_n), where='mid')

        if n == 0:
            lbl = r'$\mu$' if eig_n == 0 else r'$\mathrm{{ev}}_{{{}}}$'.format(eig_n)
            props = dict(boxstyle='square', facecolor='white', alpha=.8)
            ax.text(1., .9, lbl, verticalalignment='top', horizontalalignment='right',
                           bbox=props, fontsize='x-small')

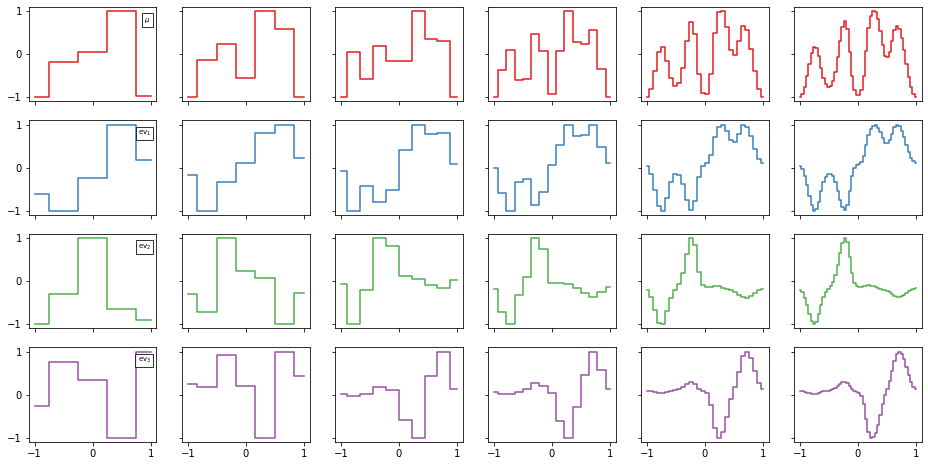
And finally, the timescales depending on the coarseness of the MSM.

length = n_eigenfunctions - 1
ys = np.arange(length)

f, ax = plt.subplots(1, 1, figsize=(8, 2))

for n, msm in enumerate(msms):
    colors = []
    for i in range(length):
        colors.append(list(cmap(i+1)))
        colors[-1][-1] = ((n+1+len(msms))/(2*len(msms)))
    ax.scatter(msm.timescales(k=length), ys, c=colors, marker='s', s=15)
ax.semilogx()
ax.set_ylim(-.5, 2.5)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.set_xlim(.91, 1.99e2)
ax.set_yticks([])

for n in range(3):
    ax.text(0.91, n, r'$\mathrm{{ev}}_{{{}}}$'.format(n+1),
             va='center', ha='left', fontsize='x-small', rotation=90)