Note
Click here to download the full example code
Custom SDEs¶
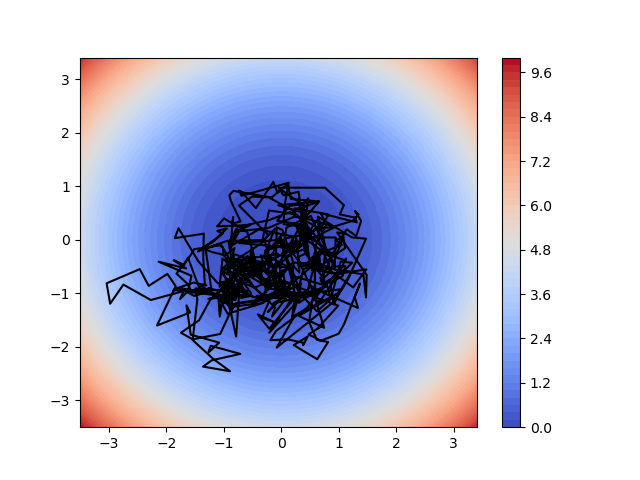
Demonstrating usage of deeptime.data.custom_sde().
One is able to define SDEs of the form
\[\mathrm{d}X_t = F(X_t) \mathrm{d}t + \sigma\mathrm{d}W_t\]
for \(X_t\in\mathbb{R}^d\), \(d\in\{1,2,3,4,5\}\).
16 import matplotlib.pyplot as plt
17 import numpy as np
18
19 from deeptime.data import custom_sde
20
21
22 def harmonic_sphere_energy(x, radius=.5, k=1.):
23 dist_to_origin = np.linalg.norm(x, axis=-1)
24 dist_to_sphere = dist_to_origin - radius
25 energy = np.zeros((len(x),))
26 ixs = np.argwhere(dist_to_sphere > 0)[:, 0]
27 energy[ixs] = 0.5 * k * dist_to_sphere[ixs] ** 2
28 return energy
29
30
31 def harmonic_sphere_force(x, radius=.5, k=1.):
32 dist_to_origin = np.linalg.norm(x)
33 dist_to_sphere = dist_to_origin - radius
34 if dist_to_sphere > 0:
35 return -k * dist_to_sphere * np.array(x) / dist_to_origin
36 else:
37 return [0., 0.]
38
39
40 sde = custom_sde(dim=2, rhs=lambda x: harmonic_sphere_force(x, radius=.5, k=1),
41 sigma=np.diag([1., 1.]), h=1e-3, n_steps=100)
42 traj = sde.trajectory([[0., 0.]], 500)
43
44 xy = np.arange(-3.5, 3.5, 0.1)
45 coords = np.dstack(np.meshgrid(xy, xy)).reshape(-1, 2)
46 potential_landscape = harmonic_sphere_energy(coords).reshape((xy.shape[0], xy.shape[0]))
47 cb = plt.contourf(xy, xy, potential_landscape, levels=50, cmap='coolwarm')
48 plt.colorbar(cb)
49
50 plt.plot(*traj.T, color='black')
Total running time of the script: ( 0 minutes 0.748 seconds)
Estimated memory usage: 8 MB
