function tv_derivative¶
- deeptime.util.diff.tv_derivative(xs, ys, u0=None, alpha=10.0, tol=None, maxit=1000, fd_window_radius=5, epsilon=1e-06, sparse=True, progress=None)¶
Total-variation regularized derivative. Note that this is currently only implemented for one-dimensional functions. See [1] for theory and algorithmic details.
(
Source code,png,hires.png,pdf)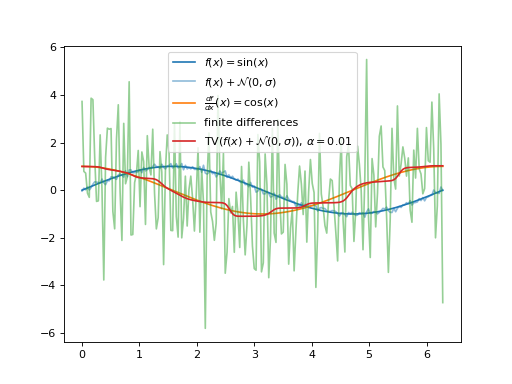
- Parameters:
xs (ndarray) – Grid points.
ys (ndarray) – Function values, must be of same length as xs.
u0 (ndarray, optional, default=None) – Initial guess. May be left None, in which case the numpy.gradient with edge_order=2 is used.
alpha (float, default=10) – Regularization parameter. Is required to be positive.
tol (float, optional, default=None) – Tolerance on the relative change of the solution update. If given, the algorithm may return early.
maxit (int, default=1000) – Maximum number of iterations before termination of the algorithm.
fd_window_radius (int, default=5) – Radius in which the finite differences are computed. For example, a value of 2 means that the local gradient at \(x_n\) is approximated using grid nodes \(x_{n-2}, x_{n-1}, x_n, x_{n+1}, x_{n+2}\).
epsilon (float, default=1e-6) – Small constant that is added to the norm of the current iterate of the TV-regularized derivative so it can safely be normalized.
sparse (bool, default=True) – Whether to use sparse matrices for finite difference, integration, and normalization operators.
progress (ProgressBar, optional, default=None) – Optional progress bar, tested for tqdm.
- Returns:
derivative – The regularized derivative values on given grid nodes.
- Return type:
ndarray
References
