function bickley_jet

deeptime.data.bickley_jet(n_particles: int, n_jobs: Optional[int] = None, seed: Optional[int] = None) → BickleyJetDataset

Simulates the Bickley jet for a number of particles. The implementation is based on [1] with parameters

\[\begin{aligned} U_0 &= 5.4138 \times \frac{10^6\mathrm{m}}{\mathrm{day}},\\ L_0 &= 1.77 \times 10^6\,\mathrm{m},\\ r_0 &= 6.371 \times 10^6\,\mathrm{m},\\ c &= (0.1446, 0.205, 0.461)^\top U_0,\\ \mathrm{eps} &= (0.075, 0.15, 0.3)^\top,\\ k &= (2,4,6)^\top \frac{1}{r_0}, \end{aligned}\]

in a domain \(\Omega = [0, 20] \times [-3, 3]\). The resulting dataset describes the temporal evolution of n_particles over 401 timesteps in \(\Omega\). The domain is periodic in x-direction. The dataset offers methods to wrap the domain into three-dimensional space onto the surface of a cylinder

\[\begin{pmatrix} x \\ y \end{pmatrix} \mapsto \begin{pmatrix} r\cdot \cos\left( 2\pi \frac{x}{20} \right) \\ r\cdot \sin\left( 2\pi \frac{x}{20} \right) \\ \frac{y}{3} \end{pmatrix},\]

with the option to further discretize the three-dimensional dataspace via binning. This way the discontinuity introduced by 2D periodicity is treated.

(Source code, png, hires.png, pdf)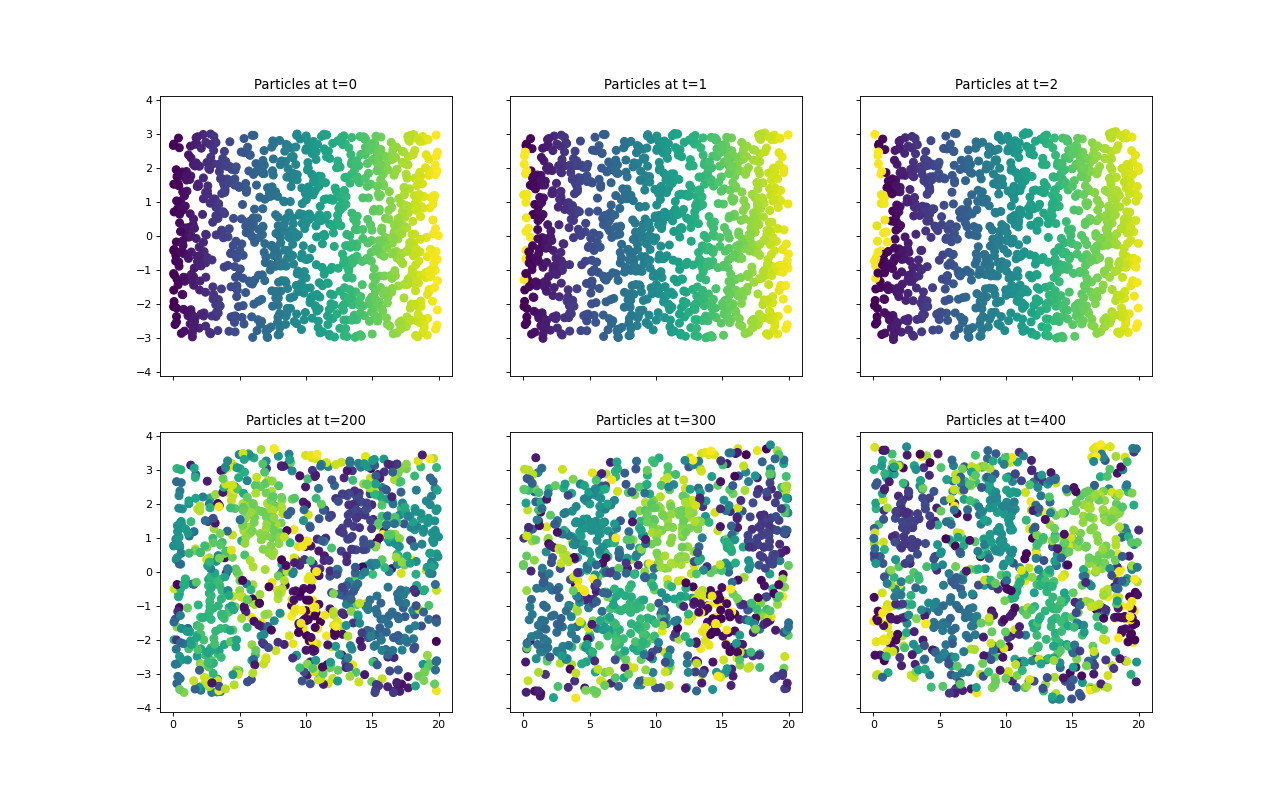

../../_images/deeptime-data-bickley_jet-1.png
Parameters:

  • n_particles (int) – Number of particles which are propagated.

  • n_jobs (int or None, default=None) – Number of threads to use for simulation.

  • seed (int or None, optional, default=None) – Random seed used for initialization of particle positions at \(t=0\).

Returns:

dataset – Dataset over all the generated frames.

Return type:

BickleyJetDataset

See also

BickleyJet

Underlying trajectory generator.

Examples

>>> import deeptime
>>> dataset = deeptime.data.bickley_jet(n_particles=5, n_jobs=1)
>>> # shape is 401 frames for 5 particles in two dimensions
>>> print(dataset.data.shape)
(401, 5, 2)

>>> # returns a timelagged dataset for first and last frame
>>> endpoints = dataset.endpoints_dataset()
>>> endpoints.data.shape
(5, 2)

>>> # maps the endpoints dataset onto a cylinder of radius 5
>>> endpoints_3d = endpoints.to_3d(radius=5.)
>>> endpoints_3d.data.shape
(5, 3)

>>> # bins the data uniformly with 10 bins per axis
>>> endpoints_3d_clustered = endpoints_3d.cluster(n_bins=10)
>>> # 5 particles and 10*10*10 bins
>>> endpoints_3d_clustered.data.shape
(5, 1000)

References