function triple_well_1d¶
- deeptime.data.triple_well_1d(h=0.001, n_steps=500)¶
A simple one-dimensional triple-well potential landscape. It is given by the stochastic differential equation
\[\mathrm{d}X_t = \nabla V(X_t) \mathrm{d}t + \sigma(t, X_t)\mathrm{d}W_t\]with \(W_t\) being a Wiener process, \(\sigma = 0.75\), and the potential \(V\) being given by
\[V(x) = 5 - 24.82 x + 41.4251 x^2 - 27.5344 x^3 + 8.53128 x^4 - 1.24006 x^5 + 0.0684 x^6.\](
Source code,png,hires.png,pdf)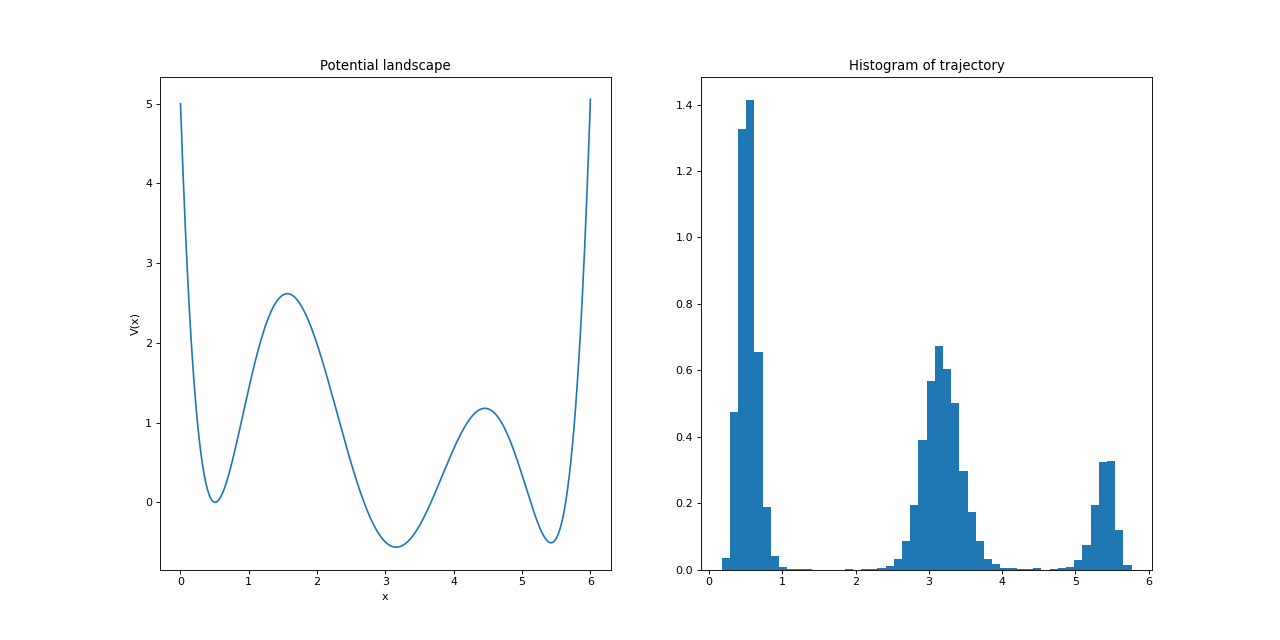
- Parameters:
h (float, default=1e-3) – Integration step size.
n_steps (int, default=500) – Default number of integration steps per evaluation.
- Returns:
system – The system.
- Return type:
