function birth_death_chain

deeptime.data.birth_death_chain(q, p, sparse=False)

Generates a birth and death chain simulator from annihilation and creation probabilities q and p.

A general birth and death chain on a d-dimensional state space has the transition matrix

$$p_{ij} = \begin{cases} q_i &\text{, if } j=i-1 \text{ and } i>0,\\ r_i &\text{, if } j=i,\\ p_i &\text{, if } j=i+1 \text{ and } i < d-1 \end{cases}$$

The annihilation probability of state $i=1$ must not be zero, same for the creation probability of the last state $i=n$. The sum of the probabilities must be bounded component-wise, i.e., $q_i + p_i \leq 1\;\forall i=1,\ldots ,n$.

(Source code, png, hires.png, pdf)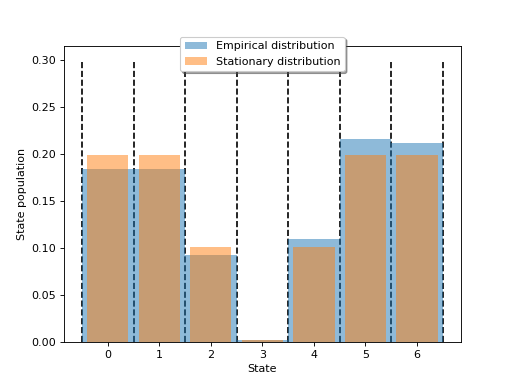

Parameters:

• q (array_like) – Annihilation probabilities for transition from i to i-1.

• p (array_like) – Creation probabilities for transition from i to i+1.

• sparse (bool, optional, default=False) – Whether to use sparse matrices.

Returns:

chain – The chain.

Return type:

deeptime.data.BirthDeathChain