function sqrt_model

deeptime.data.sqrt_model(n_samples, seed=None)

Sample a hidden state and an sqrt-transformed emission trajectory. We sample a hidden state trajectory and sqrt-masked emissions in two dimensions such that the two metastable states are not linearly separable.

(Source code, png, hires.png, pdf)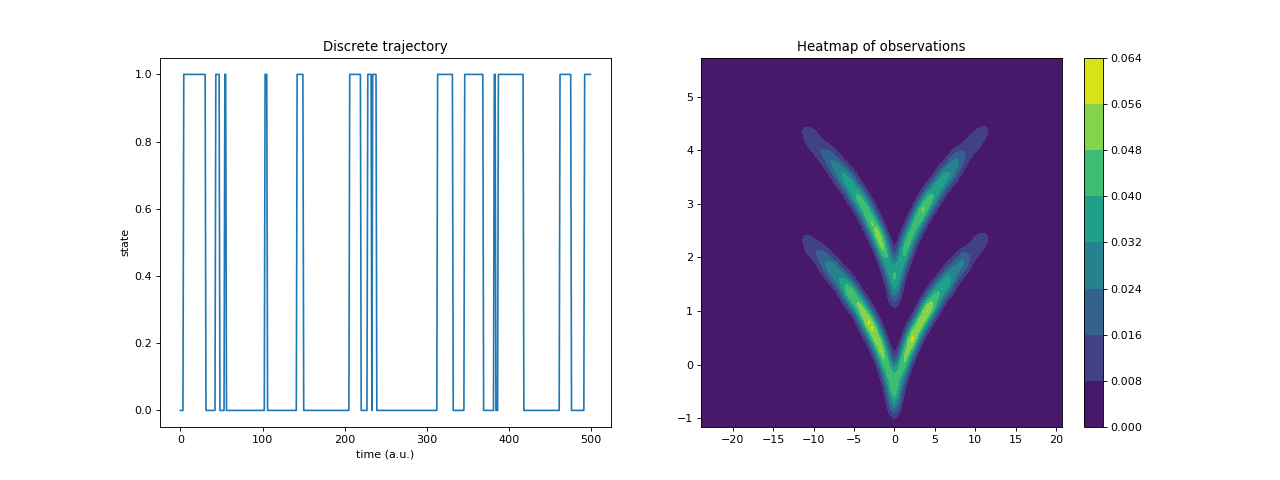

../../_images/plot_sqrt_model.png
Parameters:

  • n_samples (int) – Number of samples to produce.

  • seed (int, optional, default=None) – Random seed to use. Defaults to None, which means that the random device will be default-initialized.

Returns:

  • sequence ((n_samples, ) ndarray) – The discrete states.

  • trajectory ((n_samples, ) ndarray) – The observable.

Notes

First, the hidden discrete-state trajectory is simulated. Its transition matrix is given by

P=(0.950.050.050.95).P = \begin{pmatrix}0.95 & 0.05 \\ 0.05 & 0.95 \end{pmatrix}.

The observations are generated via the means are μ0=(0,1)⊤\mu_0 = (0, 1)^\top and μ1=(0,−1)⊤\mu_1= (0, -1)^\top, respectively, as well as the covariance matrix

C=(30000.015).C = \begin{pmatrix} 30 & 0 \\ 0 & 0.015 \end{pmatrix}.

Afterwards, the trajectory is transformed via

(x,y)↦(x,y+∣x∣).(x, y) \mapsto (x, y + \sqrt{| x |}).