Dimension reduction of double-wedge dataset¶
Here we use the double-wedge (or sqrt) model to compare some of the dimension reduction methods in a time-homogeneous setting.
[1]:
from matplotlib import pyplot as plt
import numpy as np
from tqdm.notebook import tqdm
from deeptime.data import sqrt_model
First we generate the training data with the binary classification according to wedge (dtraj) and two-dimensional state vectors (sqrt). Goal is to reconstruct dtraj from traj.
[2]:
dtraj, traj = sqrt_model(n_samples=1000, seed=777)
We can define the back-transform to make the drawn trajectory frames linearly separable according to state:
[3]:
def back_transform(x):
y = np.copy(x)
y[:, 1] = y[:, 1] - np.sqrt(np.abs(y[:, 0]))
return y
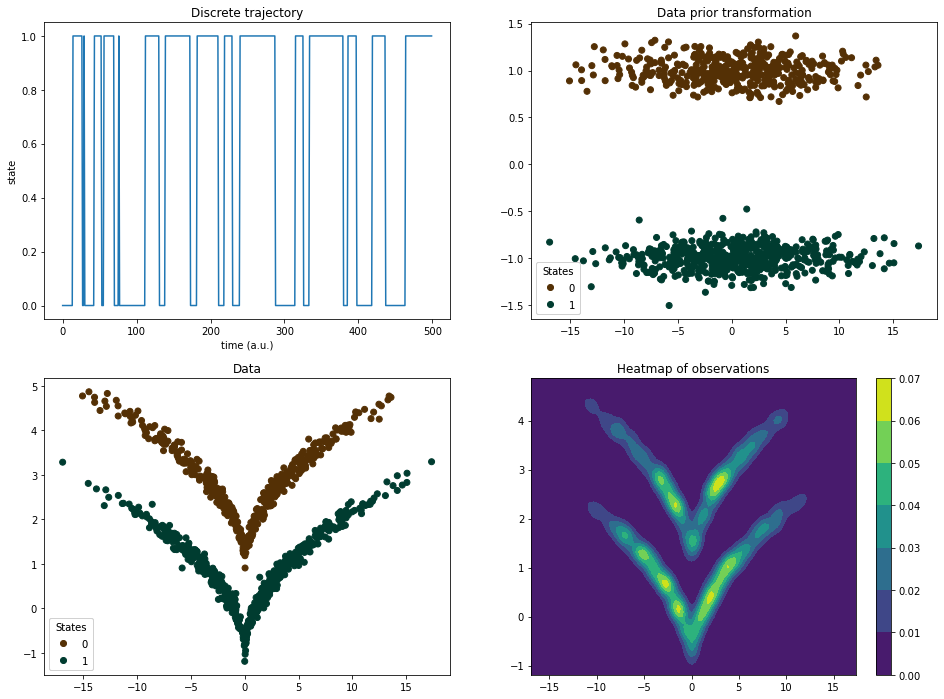
The dataset is set up as follows: The discrete trajectory (upper left panel) has corresponding two-dimensional and linearly separable datapoints (upper right panel) which are subsequently transformed through a squareroot-like function to produce the double-wedge (lower left panel).
[4]:
X, Y = np.meshgrid(
np.linspace(np.min(traj[:, 0]), np.max(traj[:, 0]), 100),
np.linspace(np.min(traj[:, 1]), np.max(traj[:, 1]), 100),
)
kde_input = np.dstack((X, Y)).reshape(-1, 2)
import scipy.stats as stats
kernel = stats.gaussian_kde(traj.T, bw_method=.1)
Z = kernel(kde_input.T).reshape(X.shape)
f, axes = plt.subplots(2, 2, figsize=(16, 12))
ax1 = axes[0, 0]
ax1.plot(dtraj[:500])
ax1.set_title('Discrete trajectory')
ax1.set_xlabel('time (a.u.)')
ax1.set_ylabel('state')
ax2 = axes[0, 1]
ax2.set_title('Data prior transformation')
scatter = ax2.scatter(*back_transform(traj).T, c=dtraj, cmap='BrBG')
legend1 = ax2.legend(*scatter.legend_elements(), title="States", loc='lower left')
ax2.add_artist(legend1)
ax3 = axes[1, 0]
ax3.set_title('Data')
scatter = ax3.scatter(*traj.T, c=dtraj, cmap='BrBG')
legend1 = ax3.legend(*scatter.legend_elements(), title="States", loc='lower left')
ax3.add_artist(legend1)
ax4 = axes[1, 1]
cm = ax4.contourf(X, Y, Z)
plt.colorbar(cm, ax=ax4);
ax4.set_title('Heatmap of observations');
Let us now compare the different methods. To this end we first define a plotting routine.
[5]:
def plot_method(transform, score, score_std):
r""" Plotting method for the different models.
Parameters
----------
transform : Callable
Function pointer that projects data into a one-dimensional space.
score
VAMP-2 score
score_std
VAMP-2 score standard deviation
"""
from deeptime.clustering import KMeans
from matplotlib.colors import Normalize
feat = transform(traj)
feat_cc = KMeans(2).fit_transform(feat)
xmax = np.max(np.abs(traj[:, 0]))
ymin = np.min(traj[:, 1])
ymax = np.max(traj[:, 1])
vmin = np.min(feat)
vmax = np.max(feat)
vmag = np.max([np.abs(vmin), np.abs(vmax)])
scatter_size = 35
grid = np.meshgrid(np.linspace(-xmax-1, xmax+1, 500), np.linspace(ymin-1, ymax+1, 500))
xy = np.dstack(grid).reshape(-1, 2)
levels = np.linspace(0, vmag, num=5)
z = np.concatenate([transform(xxyy) for xxyy in np.array_split(xy, 3)])
z00 = transform(np.array([0, -1]).reshape(-1, 2))
z = np.clip(z, vmin, vmax)
if np.mean(np.abs((feat_cc[:500].squeeze() - dtraj[:500]))) > .3:
feat_cc = 1. - feat_cc
if z00 < 0:
z *= -1.
z *= -1
cmap = 'BrBG'
f = plt.figure(figsize=(6, 6), constrained_layout=True)
height_ratios = [2, 1]
gs = f.add_gridspec(2, 1, height_ratios=height_ratios)
ax = f.add_subplot(gs[0, 0])
ax_contour = ax
norm = Normalize(-vmag, vmag)
levels_fine = np.linspace(0, levels[1], num=5)
levels = np.concatenate([-levels[2:][::-1], -levels_fine[1:][::-1], levels_fine, levels[2:]])
cb = ax.contourf(grid[0], grid[1], z.reshape(grid[0].shape), levels=levels,
cmap=cmap, norm=norm, extend='both')
ticks = levels
cb = f.colorbar(cb, ax=ax, ticks=ticks[1::3])
cb.ax.set_yticklabels([f"{x:.2f}" for x in ticks[1::3]])
ix_0 = np.where((feat_cc == 0) & (feat_cc == dtraj))[0]
ix_1 = np.where((feat_cc == 1) & (feat_cc == dtraj))[0]
ax.scatter(*traj[ix_0].T,
color=plt.cm.plasma(.3),
s=scatter_size, linewidths=.1,
marker='o', cmap=cmap, edgecolors='black',
zorder=500, alpha=.5, label=f'Estimated state {0}')
ax.scatter(*traj[ix_1].T,
color=plt.cm.plasma(.8),
s=scatter_size, linewidths=.1,
marker='o', cmap=cmap, edgecolors='black',
zorder=500, alpha=.5, label=f'Estimated state {1}')
ix_0 = np.where((feat_cc == 0) & (feat_cc != dtraj))[0]
ix_1 = np.where((feat_cc == 1) & (feat_cc != dtraj))[0]
if len(ix_0) > 0:
ax.scatter(*traj[ix_0].T,
color=plt.cm.plasma(.3),
s=scatter_size, linewidths=.5,
marker='o', cmap=cmap, edgecolors='red',
zorder=500, alpha=.5)
if len(ix_1) > 0:
ax.scatter(*traj[ix_1].T,
color=plt.cm.plasma(.8),
s=scatter_size, linewidths=.5,
marker='o', cmap=cmap, edgecolors='red',
zorder=500, alpha=.5)
ax.legend()
props = dict(boxstyle='square', facecolor='white', alpha=.8)
ax.text(0.5, 0.08, r"$s={:.2f}\pm {:.2f}$".format(score, score_std), transform=ax.transAxes,
verticalalignment='top', horizontalalignment='center', bbox=props, fontsize='x-small')
ax = f.add_subplot(gs[1, 0])
n_proj = 200
mismatch = 100. * float(np.count_nonzero(feat_cc - dtraj)) / float(len(dtraj))
rescaled_proj = .5*(feat[:n_proj] + 1)
feat_cc = feat_cc[:n_proj]
if np.mean(np.abs((rescaled_proj.squeeze() - dtraj[:n_proj]))) > .4:
rescaled_proj = 1. - rescaled_proj
xs = np.arange(len(rescaled_proj))
ax.plot(xs, rescaled_proj, alpha=.3, color='C0')
ax.plot(xs, feat_cc, color='C0', label=r'Estimated (${:.1f}\%$ mismatch)'.format(mismatch))
ax.plot(xs, dtraj[:n_proj], color='C1', linestyle='dotted', label='Ground truth')
ax.set_xlabel('time (a.u.)')
ax.set_ylabel(r'$\chi (x_t)$')
ax.set_ylim([-.5, 1.5])
ax.set_yticks([0, 1])
ax.set_title(r"${:.1f}\%$ acc.".format(100-mismatch))
ax.legend(loc="lower center", ncol=2)
return ax_contour, ax
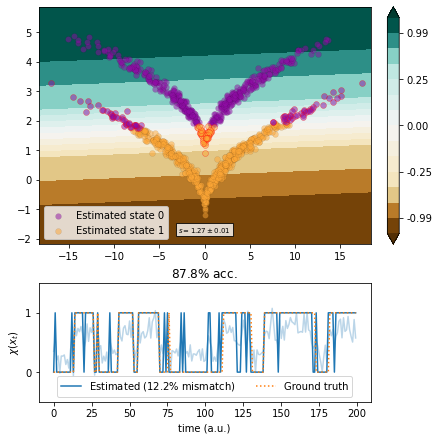
TICA¶
We use the linear TICA method.
[6]:
from deeptime.decomposition import vamp_score_cv
from deeptime.decomposition import TICA
estimator = TICA(lagtime=1, dim=1)
tica = estimator.fit_fetch(traj)
scores = vamp_score_cv(estimator, traj, blocksize=100, random_state=42)
plot_method(tica.transform, scores.mean(), scores.std());
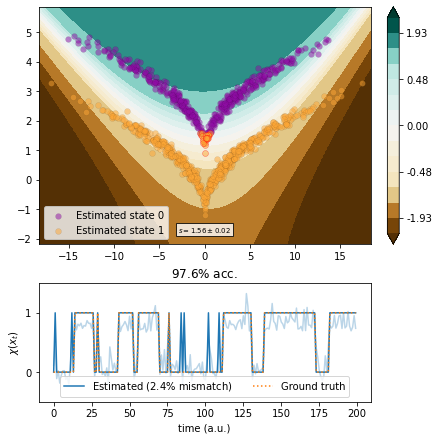
EDMD¶
We use EDMD with a polynomial ansatz basis of degree up to \(2\).
[7]:
from deeptime.decomposition import EDMD, VAMP
from deeptime.basis import Monomials
basis = Monomials(p=2, d=2)
edmd = EDMD(basis=basis).fit_fetch(traj, lagtime=1)
vamp_edmd = VAMP(lagtime=1, dim=1,
observable_transform=lambda x: edmd.transform(x).real)
scores = vamp_score_cv(vamp_edmd, traj, blocksize=100, random_state=42)
plot_method(lambda x: edmd.transform(x)[..., 1].real, scores.mean(), scores.std())
[7]:
(<AxesSubplot:>,
<AxesSubplot:title={'center':'$97.6\\%$ acc.'}, xlabel='time (a.u.)', ylabel='$\\chi (x_t)$'>)
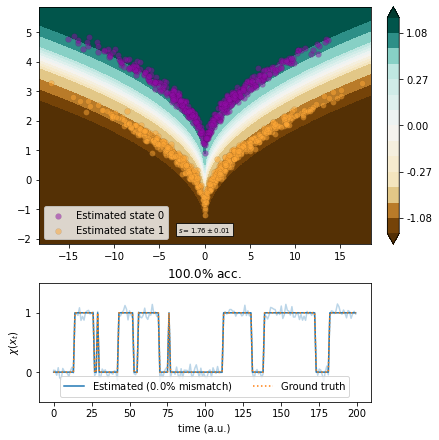
VAMP with backtransform¶
We use VAMP with knowledge about the ground truth to make data linearly separable.
[8]:
vamp_back = VAMP(lagtime=1, dim=1,
observable_transform=back_transform).fit(traj)
scores = vamp_score_cv(vamp_back, traj, blocksize=100, random_state=42)
plot_method(vamp_back.transform, scores.mean(), scores.std());
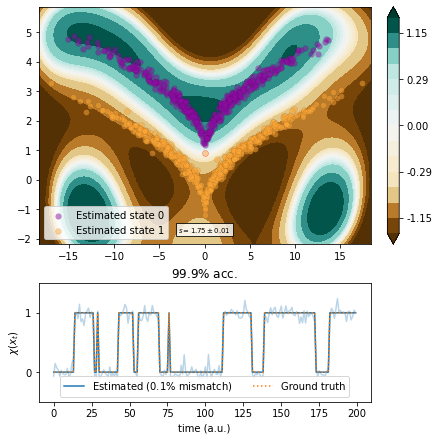
Kernel EDMD¶
We use kernel EDMD with a Gaussian kernel and parameter optimization in whitened space.
[9]:
from deeptime.covariance import Covariance
cov = Covariance(lagtime=1, compute_c0t=True).fit(traj).fetch_model()
whitened_traj = cov.whiten(traj)
[10]:
from deeptime.kernels import GaussianKernel
from deeptime.decomposition import KernelEDMD
kernel = GaussianKernel(1.4)
kedmd = KernelEDMD(kernel=kernel, epsilon=1.6e-3, n_eigs=2).fit_fetch(whitened_traj, lagtime=1)
kedmd_transf = lambda x: (kedmd.transform(cov.whiten(x)).real).reshape(-1, 2)
vamp_kedmd = VAMP(lagtime=1, dim=1, epsilon=1e-16, observable_transform=kedmd_transf).fit(traj)
scores = vamp_score_cv(vamp_kedmd, traj, blocksize=100, random_state=42)
plot_method(vamp_kedmd.transform, scores.mean(), scores.std());
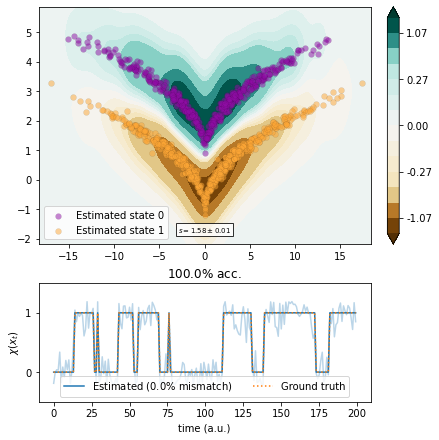
Kernel CCA¶
We use kernel CCA with optimized kernel parameters.
[11]:
from deeptime.decomposition import KernelCCA
from scipy.optimize import Bounds, minimize
def objective(params):
bw, eps = params
kcca = KernelCCA(GaussianKernel(bw), 1, epsilon=eps).fit((traj[:-1], traj[1:])).fetch_model()
vamp_kcca = VAMP(lagtime=1, dim=1,
observable_transform=lambda x: kcca.transform(x).real).fit(traj).fetch_model()
return -vamp_kcca.score(2)
bounds = Bounds([1e-2, 1e-2], [1e-0, 1e-0])
result = minimize(objective, x0=[.8, .3], bounds=bounds, method='SLSQP')
bw, eps = result.x
print(f"Estimated bandwidth {bw:.3e} and regularization parameter {eps:.3e}.")
Estimated bandwidth 8.551e-01 and regularization parameter 1.000e-02.
[12]:
kernel = GaussianKernel(bw)
kcca = KernelCCA(kernel, 1, epsilon=eps).fit_fetch(traj, lagtime=1)
kcca_transform = lambda x: kcca.transform(x).real
vamp_kcca = VAMP(lagtime=1, dim=1, observable_transform=kcca_transform).fit(traj)
scores = vamp_score_cv(vamp_kcca, traj, blocksize=100, random_state=42)
plot_method(vamp_kcca.transform, scores.mean(), scores.std());
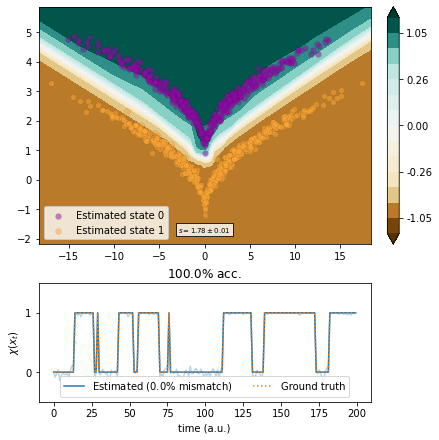
VAMPNets¶
We use VAMPNets with a multilayer preceptron (MLP) architecture.
[13]:
import torch.nn as nn
from torch.utils.data import DataLoader
from deeptime.util.data import TrajectoryDataset
from deeptime.util.torch import MLP
from deeptime.decomposition.deep import VAMPNet
dataset = TrajectoryDataset(1, traj.astype(np.float32))
estimator = VAMPNet(lobe=MLP(units=[traj.shape[1], 15, 10, 10, 5, 1], nonlinearity=nn.ReLU),
learning_rate=1e-3)
loader_train = DataLoader(dataset, batch_size=128, shuffle=True)
vampnet = estimator.fit_fetch(loader_train, n_epochs=170, progress=tqdm)
[14]:
vamp_vampnet = VAMP(lagtime=1, dim=1, observable_transform=vampnet).fit(traj)
scores = vamp_score_cv(vamp_vampnet, traj, blocksize=100, random_state=42)
plot_method(vamp_vampnet.transform, scores.mean(), scores.std());
Markov state models¶
We use MSMs with a box discretization of various degrees of fineness.
[15]:
from deeptime.clustering import BoxDiscretization
from deeptime.markov import TransitionCountEstimator
from deeptime.markov.msm import MaximumLikelihoodMSM
def estimate(n_boxes):
clustering = BoxDiscretization(dim=2, n_boxes=n_boxes).fit_fetch(traj)
counts = TransitionCountEstimator(lagtime=1, count_mode='sliding', n_states=clustering.n_clusters).fit_fetch(clustering.transform(traj)).submodel_largest()
msm = MaximumLikelihoodMSM(lagtime=1).fit_fetch(counts)
def transform(xy):
dtr = clustering.transform(xy)
dtr = msm.count_model.transform_discrete_trajectories_to_submodel(dtr)
evr = msm.eigenvectors_right(2)
invalids = dtr == -1
output = np.empty(shape=(len(dtr), 2))
output[invalids, :] = 0
output[~invalids, :] = evr[dtr[~invalids]]
return output
vamp_msm = VAMP(lagtime=1, dim=1, observable_transform=transform).fit(traj)
scores = vamp_score_cv(vamp_msm, traj, blocksize=10, random_state=42)
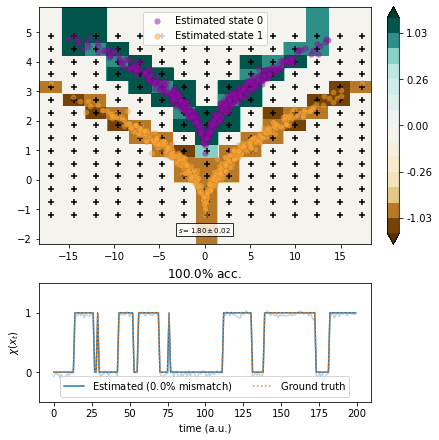
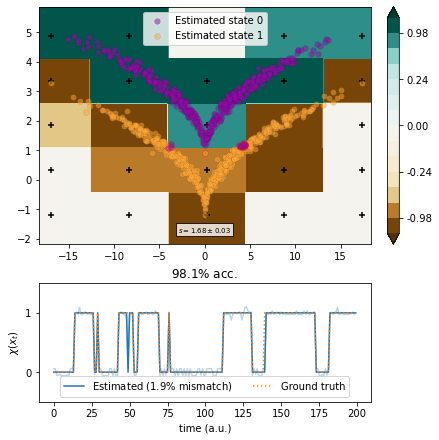
ax, _ = plot_method(vamp_msm.transform, scores.mean(), scores.std())
ax.scatter(*clustering.cluster_centers.T, color='black', marker='+')
[16]:
estimate(5)
[17]:
estimate(7)
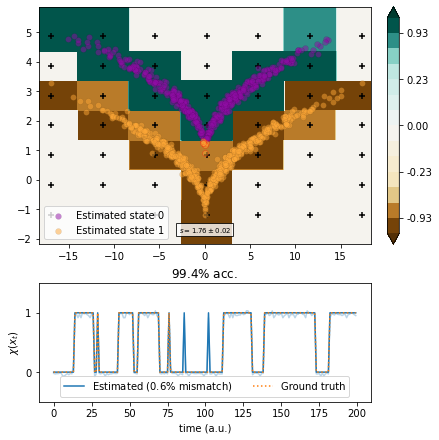
[18]:
estimate(15)