function custom_ode

deeptime.data.custom_ode(dim: int, rhs: Callable, h: float, n_steps: int)

This function allows the definition of custom ordinary differential equations (ODEs) of the form

\[\mathrm{d}X_t = F(X_t) \mathrm{d}t,\]

where the right-hand side \(F\) should map an dim-dimensional array-like object to an dim-dimensional array-like object.

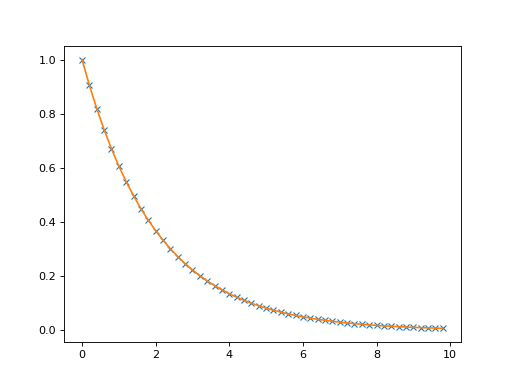
Parameters:

  • dim (int, positive and less or equal to 5) – The dimension of the SDE’s state vector \(X_t\). Must be less or equal to 5.

  • rhs (Callable) – The right-hand side function \(F(X_t)\). It must map a dim-dimensional array like object to a dim-dimensional array or list.

  • h (float) – Step size for the Runge-Kutta integrator.

  • n_steps (int) – Number of integration steps per evaluation / recording of the state.

Returns:

system – The system.

Return type:

CustomSystem

Examples

First, some imports.

>>> import numpy as np
>>> import deeptime as dt

We can define the right-hand side to model an exponential decay

>>> def rhs(x):
...     return [-.5 * x[0]]

and obtain the system

>>> system = dt.data.custom_ode(dim=1, rhs=rhs, h=1e-3, n_steps=20)

where n_steps is the number of (Runge-Kutta 45) integration steps per evaluation and h the step-size. With the system, one can generate trajectories

>>> traj = system.trajectory(x0=[[1.]], length=50, seed=45)
>>> assert traj.shape == (50, 1)

as well as propagate sample points by n_steps:

>>> propagated_samples = system(np.random.uniform(size=(100, 1)))
>>> assert propagated_samples.shape == (100 ,1)